一文理解 HyperLogLog(HLL) 算法

发表于 2022-11-29 分类于技术阅读次数：

HyperLogLog(HLL) 算法是一种估算海量数据基数的方法，被广泛用于各个数据库产品中。

与精确的基数统计算法相比，HLL 具备可合并性 (mergeability) ，因而可以方便地对海量数据进行并行计算，被广泛地用于大数据多维分析场景中。例如分别统计一款 APP 每个小时的 UV 以及全天的 UV，这类问题就非常适合使用 HLL 算法。

本文将会由浅入深，从基本概念讲起，引导读者从直观上理解 HLL 算法背后蕴含的基本思想。

基数统计

基数 (Cardinality) 是指一个字段所包含的不同取值的个数，有时候也称为 Distinct Values，简写为 DV。

举个例子：

序列 [1, 2, 3, 4] 的基数为 4，因为包含 4 个不同的取值。
序列 [1, 2, 3, 1, 2] 的基数为 3，虽然包含 5 个元素，但其中的 1, 2 分别重复了一次。

最直观的基数统计方法是利用 HashSet：将序列中的所有值依次添加到 HashSet 中，最后统计 HashSet 中值的个数即可。用 Python 代码实现如下：

def get_dv(stream):
    s = set()
    for value in stream:
        s.add(value)
    return len(s)

既然如此，为什么我们不使用 HashSet 来计算基数呢？

原因在于计算成本。当要统计的数据非常多时，HashSet 将会占用很大的内存，以至于资源耗尽也无法完成计算，这种情况在大数据场景下非常常见。在 HashSet 的基础上，有一个可以节省资源的改进方案，就是采用 bitmap，但 bitmap 只是把问题延缓了，仍然没有根本性地解决问题。

事实上，我们统计基数时往往并不要求分毫不差，只需要给出一个具有误差边界的粗略值即可。那么在这种前提下能否节省计算资源呢？

HyperLogLog(HLL) 就是这样一种算法，可以在计算结果的精确程度和资源占用之间取得一种平衡。

让我们从一些浅显的问题着手，逐步揭开 HLL 算法的神秘面纱。

从概率视角看计数方法

常规的计数方法会维护一个列表，每到来一条数据记录一下。这种计数是精确的，但代价是必须维护一个越来越长的列表。

概率论为我们提供了另外一种看待计数的视角：

$$ 观测到小概率事件发生（概率 p） → 类似的事情重复过很多次了（次数 N）$$

其中蕴含着一个粗略的定量关系：

$$N = 1/p$$

举个例子：

在摇骰子猜大小的游戏中，三个骰子同时为 6 点的概率很小，为 1/(6^3)。假如在某场游戏中摇出了三个 6 点，猜猜一共摇了几次？

答：大概 6^3=216 次

更进一步的例子：

有一个抛硬币游戏，规则如下：玩家每次抛掷一枚均匀的硬币，正面与反面朝上的概率均> 为 1/2，每次抛掷都记一分。如果正面朝上，则继续抛掷；如果反面朝上，则游戏结> 束。

问1：在一局游戏中得 5 分的概率是多少？
答1：得 5 分意味着抛掷序列为「正正正正反」，概率为 (1/2)^5 = 1/32

问2：在一组游戏中，最高得分是 5 分，请问玩了多少局？
答2：大概 32 局

如果把硬币的正反两面分别记作 0、1 的话，那么 HyperLogLog 的计数原理就呼之欲出了：

对于每一条待统计的数据（例如 user_id），计算其 hash 值并写成二进制形式（0-1 串），然后将其看作一局抛硬币游戏的记录，其中：

0 代表硬币正面朝上。
1 代表硬币反面朝上。

例如 hash(uid_345678)=00010010，意味着这局抛硬币游戏出现连续 3 次正面朝上，第 4 次反面朝上，游戏结束，最终得分为 4。第 4 位以后的序列不影响得分，可以忽略。

按照上述步骤，计算每条数据对应的「得分」，并找出其中的最高分 μ。那么这组数据的基数的期望为：

$$N = 2^μ$$

这就是利用概率论来估算基数所依据的基本原理。

在上述过程中涉及了一个重要步骤，就是将每个待观察的数据进行 hash 操作。为什么需要 hash 操作，而不是直接观察数据本身对应的二进制串呢？

这是因为游戏要求每次取 0 或 1 的概率是均等的，都是 0.5（这样整局游戏是一个伯努利过程）。换言之，要确保观察的 0-1 串足够随机才行。如果不做 hash 的话则无法保证随机性，例如对于 int 类型的数据，较小的值如 0、1、2 的二进制串中包含很长的连续 0，导致得分很高，这显然是错误的。

HLL 中实际使用的 hash 算法为 MurmurHash，其主要优势是随机性强和快速。

此外，比特币中使用 hash 值的前导零的个数来定义挖矿时的难度值 Difficulty，其蕴含的思想是完全相同的。前导零个数越多，意味着要尝试的 hash 计算次数越多，对应着基数越大，其工作量/难度也越高。

MVP 版基数估计算法

根据上面的讨论，实现一个简单的基数估计算法如下：

def get_dv(stream):
    max_z = 0
    for value in stream:
        h = murmur_hash(value)
        z = leading_zeros_count(h)
        if z > max_z:
            max_z = z
    return 1 << (max_z + 1)

这个算法足够简单，而且理论上是没问题的。但实际上在数据量较小的情况下误差非常大，因为前导零个数的偶然性太大了。就好比抛硬币总是容易出现某一次运气爆棚的情况，严重拉高总体的估算值。

设想一下，假设仅输入一条数据，这个数据刚好有 1 个前导零，那么最终估计出的基数为 2^(1+1)=4，如果刚巧遇到更多的前导零，那么偏差会更大。最关键的是，这些偏差无法靠算法本身来控制，准确度全靠运气。

LogLog 算法

为了解决 MVP 算法不稳定、运气成分大的问题，一种最简单的思路就是「分拆计算求平均值」，也就是把输入数据均分为 $m$ 份（称为桶），每一个桶分别应用 MVP 算法，最终得分 $\bar{\mu}$ 为各桶得分的平均值。这就是 LogLog 算法所采用的思路，LogLog 是早于 HyperLogLog 诞生的一种算法。

LogLog 算法的计算公式可表示为：

$$N=\alpha \cdot m \cdot 2^{\bar{\mu}}$$

其中，$m$ 为分桶个数，$\bar{\mu}$ 为各桶最高得分的平均值，$\alpha$ 为修正系数，用于修正算术平均数带来的系统偏差。$\alpha$ 的计算规则如下：

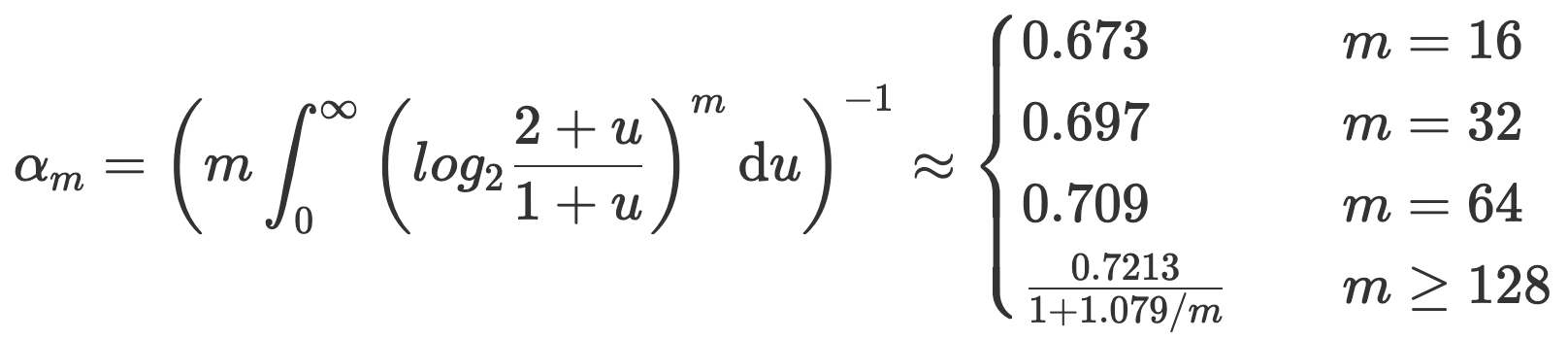
根据算法的特点，通常将分桶数 $m$ 设为 2 的整数次幂。例如 $m=64=2^6$，此时可以通过 hash 值的前 6 个 bit 来表示桶编号。从第 7 个 bit 开始统计前导零个数。

HyperLogLog 算法

LogLog 算法通过「分桶求平均值」的方式提高了估算结果的稳定性，使得算法更能抵御偶然性带来的影响。

但这么做仍然不够，因为算术平均数有一个天然的缺陷，就是容易受到极大/极小值的影响，一个离群点可能把最终结果严重带偏。例如老板月入 100000 元，9 个员工均月入 3000 元，那么平均收入就是 (100000+3000*9)/10=12700 元，这距离群里中的大多数（即 9 个员工）相差甚远，不能反映普遍情况。

如果将算术平均数改为调和平均数就可以解决这个问题，调和平均数的计算公式如下：

$$\bar{x}=\frac{1}{\frac{1}{n}\sum_n\frac{1}{x_i}} = \frac{n}{\sum_n\frac{1}{x_i}}$$

使用调和平均数计算出的平均收入为 10/(1/100000+9/3000)=3322，比较接近群体中的普遍情况。

HyperLogLog 算法对于 LogLog 算法的重要改进就是把算术平均数改成了调和平均数。同时，HLL 不是先求平均得分，再计算指数（因为这会导致离群点的效应指数级放大），而是先计算出每个桶的基数，然后求调和平均数。

HLL 统计基数的公式如下：

$$ N=\alpha\cdot m \cdot \frac{m}{\sum_{i=1}^m \frac{1}{2^{\mu_i}}} $$

在实际使用中，为了提高小样本的准确度，HLL 在上述公式计算结果的基础上还进行了一次修正。完整计算流程参见下图：

前面提到过，分桶数越多越能抵御偶然效应带来的影响，使得基数估计的结果更准确。那么可以想到，HLL 算法的估算精度（用相对标准误差 RSD 来表示）与分桶数 m 之间存在负相关关系。其定量关系如下：

$$RSD = \frac{1.04}{\sqrt{m}}$$

有了这个关系，我们可以轻易地通过想要达到的误差精度来决定分桶的个数。

合并

HLL 算法的一个重要特点是可合并性，使其能够预先统计各个子集的基数，然后汇总得到总体基数，极大地提高了统计效率。

HLL 结构体的合并过程非常简单，这是因为每个 HLL 结构体本质上就是一个桶数组。假设要将桶数组 a 和 b 合并成桶数组 c，只需要从 a、b 的对应位置取最大值即可，使用 Python 代码描述如下：

def hll_merge(a, b):
    m = len(a)
    c = [0]*m
    for i in range(m):
        c[i] = max(a[i], b[i])
    return c

合并后的桶数组按照上文中的公式估算基数即可。

示例

Rob Grzywinski 创建了一个 HyperLogLog 算法的 demo 网站，可以直观地理解算法的计算过程。

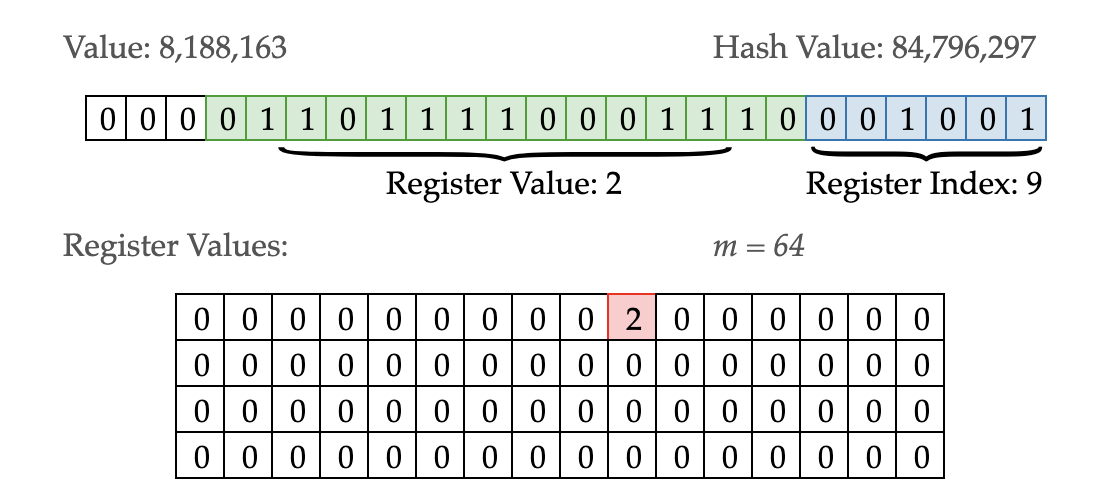
下图中显示，输入数据 value=8188163，其 MurmurHash 值为 84796297，二进制串见图。此外，图中 m=64 代表有 64 个桶，每个桶中的最高得分维护在一个表格中。

二进制串的最后 6 bit 用于表示桶 (Register) 编号，即 001001(9)，所以当前数据划到第 9 桶。为什么用 6 bit 表示桶编号？因为这样刚好足够区分 64 个桶。如果要求桶数更多，则相应地需要更多 bit。

紧接着的 15 bit 用于统计得分（从右端开始），本例中得分为 2，因此第 9 个桶中记录 2。为什么只统计 15 个 bit 呢？因为工程实现中 register 结构体是有空间限制的，此处每个 register 占用 4 bit，记录范围为 0~15，所以能容纳的最大数字就是 15，如果得分大于 15 就记录不上了。

可以想象，每个桶占用 4 bit 的话能够统计的数据量非常有限，当所有桶的得分都为 15 时达到上限，约为 0.709*64*2^15=1486880 个。但考虑到整个 HLL 结构体仅占用了 64*4bit=32byte 的存储，空间效率是非常惊人的。

从上面的推导中可以看到，一个 HLL 结构体所能统计的基数范围与它占用的空间存在两重 Log 关系，这也是算法被称为 LogLog 的原因。

回到上面的例子就是，基数容量 $1486880 ∝ 2^{2^4}$，其中的"4"代表每个桶占用 4bit 空间。

业界案例

在工程实践中，HLL 结构体的桶数和容量通常是可调参数，当数据量增大或者要求更高的精确度时，可以调高容量。

下面列出一些业界使用 HLL 算法的例子：

1 . Apache DataSketch

Apache DataSketch 算法族中包含 HyperLogLog 的实现，该算法族被广泛用于许多大数据基础组件中，用于支持基数、分位数等的快速计算。例如：

Hive/Spark 通过官方 UDXF 的方式使用 DataSketch；
Apache Druid 通过官方插件的形式引入 DataSketch 扩展；
PostgreSQL 也通过插件形式引入 DataSketch 算法。

2 . Redis

Redis 中使用 PFCOUNT 命令来调用 HLL 算法。

其 HLL 结构使用了 2^14=16384 个桶，hash 值采用 64bit 表示，除了桶编号之外剩余的 50 bit (64-14=50) 全部用于统计得分。为了确保桶中记录的分数最大范围高于 50，每个桶需要占用 6 bit 空间（2^6>50）。这样，总体的空间占用为 16384*6bit=12KB。

当数据量很少时会存在大量的空桶，此时出于优化目的，可以借助稀疏存储的表示方法来压缩空间，能够取得数倍到上千倍的压缩率。

3 . ClickHouse

ClickHouse 中的 uniq 函数背后采用的是 HLL 算法。

4 . Doris
Doris 中 approx_count_distinct 函数背后采用的也是 HLL 算法。原理类似，不再赘述。

Henry's Blog